Properties of polygons and polyhedra

Introduction

This is a list of distances, areas and angles regarding some 2D and 3D shapes.

Polygons

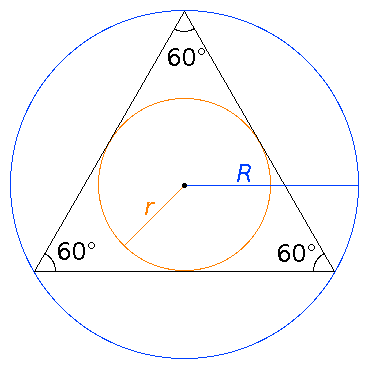
an equilateral triangle; circumcircle and circumradius in blue; incircle and inradius in orange

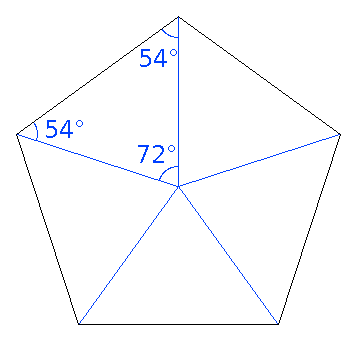
a regular pentagon divided into five equal isosceles triangles

The table shows the name, circumradius R and inradius r for various regular polygons (all angles equal) with n sides, each of length one. The first row after the headers (n=any) has general formulas that work with any such polygon.

`n`	Name	Circumradius	Inradius
any	`n`-gon	1 / (2 × sin(180° / `n`))	1 / (2 × tan(180° / `n`))
3	triangle	√3 / 3	√3 / 6
4	square	√2 / 2	1 / 2
5	pentagon	√((5 + √5) / 10)	√(25 + 10√5) / 10
6	hexagon	1	√3 / 2
8	octagon	1 / √(2 − √2)	(1 + √2) / 2
10	decagon	(1 + √5) / 2	√(5 + 2√5) / 2
12	dodecagon	(√6 + √2) / 2	(2 + √3) / 2
15	penta(kai)decagon	(√3 + √(5 + 2√5)) / 2	√(7 + 2√5 + 2√(15 + 6√5)) / 2
16	hexa(kai)decagon	1 / √(2 − √(2 + √2))	(1 + √2 + √(4 + 2√2)) / 2
20	icosagon	2 / √(8 − √(40 + 8√5))	(1 + √5 + √(5 + 2√5)) / 2
24	icosi(kai)tetragon	1 / √(2 − √(2 + √3))	(2 + √2 + √3 + √6) / 2
30	triacontagon	(2 + √5 + √(15 + 6√5)) / 2	1 / (2√(7 − 2√5 − 2√(15 − 6√5)))
32	triaconta(kai)digon	1 / √(2 − √(2 + √(2 + √2)))	√(1 / (2 − √(2 + √(2 + √2))) − 1 / 4)
48	tetraconta(kai)octagon	1 / √(2 − √(2 + √(2 + √3)))	√(1 / (2 − √(2 + √(2 + √3))) − 1 / 4)
60	hexacontagon	2 / √(8 − √3 − √15 − √(10 − 2√5))	√(4 / (8 − √3 − √15 − √(10 − 2√5)) − 1 / 4)

How R and r depend on each other:

R = √(r² + 1 / 4)
r = √(R² − 1 / 4)

Other properties of regular n-gons:

area from number of sides and inradius: A = nr / 2 = n / (4 × tan(180° / n))
internal angle between two sides: 180° × (n − 2) / n
distance between two opposite vertices (for even n): 2R
distance between centres of two opposite sides (for even n): 2r
distance between vertex and centre of opposite side (for odd n): R + r
distance between two different vertices that are adjacent to the same vertex (for n ≥ 4): 2 × cos(180° / n)

A regular n-gon can be split into n similar isosceles triangles which meet at the centre of the polygon (see image); each triangle has:

two angles of 90° × (n − 2) / n and one of 360° / n
two sides of length R and one of length 1
height r

Polyhedra

Some regular polyhedra with edge length one.

Faces: e.g. 8×3+6×4 means 8 triangles and 6 squares. Circumradius, midradius and inradius: radius of circumsphere, midsphere and insphere, respectively; they touch each vertex, edge and face once, respectively.

Name	Faces	Circumradius	Midradius	Inradius
tetrahedron	4×3	√6 / 4	√2 / 4	√6 / 12
octahedron	8×3	√2 / 2	1 / 2	√6 / 6
dodecahedron	12×5	(√3 + √15) / 4	(3 + √5) / 4	√((25 + 11√5) / 10) / 2
icosahedron	20×3	√((5 + √5) / 2) / 2	(1 + √5) / 4	(3√3 + √15) / 12

Properties of polygons and polyhedra

Introduction

Polygons

Polyhedra

Sources

See also