Tietoa kolmioista
Johdanto
Tällä sivulla esitellään erilaisia kolmiotyyppejä.
Kolmioihin on merkitty:
- sivut pienillä latinalaisilla kirjaimilla a, b ja c
- kulmat pienillä kreikkalaisilla kirjaimilla α (alfa), β (beta) ja γ (gamma).
Kulman α on oltava sivua a vastapäätä, kulman β sivua b vastapäätä ja kulman γ sivua c vastapäätä. Jos tätä sääntöä ei noudateta, osa kaavoista ei toimi.
Kolmion korkeus jostakin sivusta laskettuna on lyhin etäisyys siitä vastakkaiseen kärkeen. Esimerkiksi ha on korkeusjana, joka on kohtisuorassa sivuun a nähden.
Tämä sivu on hieman kesken varsinkin piirrosten osalta. Wikipediasta myös löytynee samat kaavat varmemmin oikein. Laitoin tämän nyt kuitenkin nettiin jotta motivoituisin joskus päivittämään sitä ja siinä sivussa oppimaan jotain.
Tasakylkinen suorakulmainen kolmio
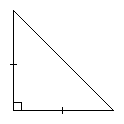
- englanniksi isosceles right triangle
- tässä c on pisin sivu
- sivujen pituudet: a = b; c = √(2) × a
- kulmat: α = β = 45°; γ = 90°
- pinta-ala: A = a2 / 2
Suorakulmainen kolmio
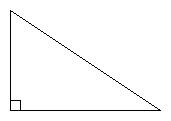
- englanniksi right triangle
- yksi kulma on 90°
- tässä c on pisin sivu
- englanninkielinen muistisääntö trigonometrisille funktioille: SOHCAHTOA:
- Sine = Opposite / Hypotenuse (kulman sini = kulman vastainen sivu / pisin sivu)
- Cosine = Adjacent / Hypotenuse (kulman kosini = kulman viereinen sivu / pisin sivu)
- Tangent = Opposite / Adjacent (kulman tangentti = kulman vastainen sivu / kulman viereinen sivu)
| Kaava | Kuvaus |
|---|---|
|
a = √(c2 − b2); b = √(c2 − a2); c = √(a2 + b2) |
sivun pituus muiden sivujen pituuksista (Pythagoraan lause) |
|
α = 90° − β; β = 90° − α |
kulma toisesta kulmasta |
|
a = c × sin(α) = c × cos(β) = b × tan(α) = b / tan(β); b = c × sin(β) = c × cos(α) = a × tan(β) = a / tan(α); c = a / sin(α) = a / cos(β) = b / sin(β) = b / cos(α) |
sivun pituus kulmasta ja toisen sivun pituudesta |
|
α = arcsin(a / c) = arccos(b / c) = arctan(a / b); β = arcsin(b / c) = arccos(a / c) = arctan(b / a) |
kulma kahden sivun pituudesta |
| A = a × b / 2 | pinta-ala kahden sivun pituudesta |
| hc = ? | korkeus |
Tasasivuinen kolmio
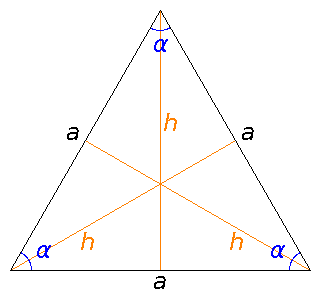
- englanniksi equilateral triangle
- kaikki sivut yhtä pitkiä
- jokainen kulma 60°
- kaikki korkeudet yhtä suuria
| Kaava | Kuvaus |
|---|---|
| h = √(3) / 2 × a | korkeus sivun pituudesta |
| A = a × h / 2 | pinta-ala sivun pituudesta ja korkeudesta |
| A = √(3) / 4 × a2 | pinta-ala sivun pituudesta |
Tasakylkinen kolmio
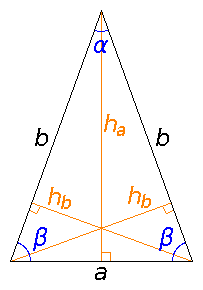
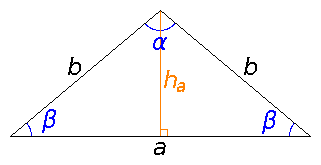
- englanniksi isosceles triangle
- teräväkulmaisessa (vasemmalla) α < 90° ja tylppäkulmaisessa (oikealla) α > 90°
- kaksi yhtä pitkää sivua b
- kaksi yhtä suurta kulmaa β
- Wikipedia – tasakylkinen kolmio
| Kaava | Kuvaus |
|---|---|
|
α = 180° − 2 × β; β = (180° − α) / 2 |
kulma toisesta kulmasta |
|
ha = √(b2 − a2 / 4); hb = a × √(b2 − a2 / 4) / b |
korkeus sivujen pituuksista |
|
ha = sin(β) × b = tan(β) × a / 2 = cos(α / 2) * b = a / 2 / tan(α / 2); hb = sin(α) × b = sin(β) × a |
korkeus yhden sivun pituudesta ja yhdestä kulmasta |
|
A = a × ha / 2 = b × hb / 2 |
pinta-ala yhden sivun pituudesta ja sitä vastaavasta korkeudesta |
Yleinen kolmio
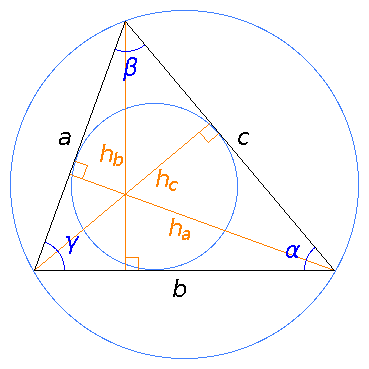
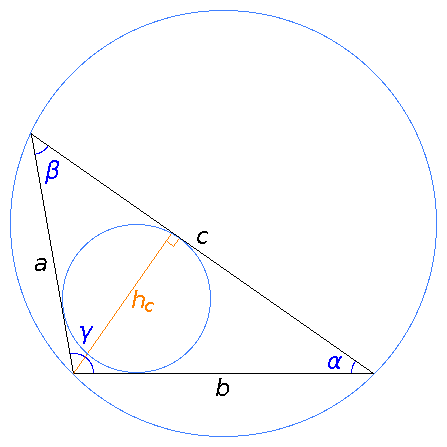
- englanniksi scalene triangle
- kaikki sivut voivat olla eri pituisia
- kaikki kulmat voivat olla eri suuria
- Wikipedia – kosinilause
| Kaava | Kuvaus |
|---|---|
|
α = 180° − β − γ; β = 180° − α − γ; γ = 180° − α − β |
kulma kahdesta muusta kulmasta |
|
ha = sin(β) × c = sin(γ) × b; hb = sin(α) × c = sin(γ) × a; hc = sin(α) × b = sin(β) × a |
korkeus yhden sivun pituudesta ja yhdestä kulmasta |
|
a = √(b2 + c2 − 2 × cos(α) × b × c); b = √(a2 + c2 − 2 × cos(β) × a × c); c = √(a2 + b2 − 2 × cos(γ) × a × b) |
sivun pituus sen vastaisesta kulmasta ja muiden sivujen pituuksista (kosinilause) |
|
α = arccos((b2 + c2 − a2) / (2 × b × c)); β = arccos((a2 + c2 − b2) / (2 × a × c)); γ = arccos((a2 + b2 − c2) / (2 × a × b)) |
kulma kaikkien sivujen pituuksista (kosinilause) |
| p = (a + b + c) / 2; A = √(p × (p − a) × (p − b) × (p − c)) |
pinta-ala kaikkien sivujen pituuksista (Heronin kaava) |
| A = a × ha / 2 = b × hb / 2 = c × hc / 2 |
pinta-ala korkeudesta ja sitä vastaavan sivun pituudesta |
| A = sin(α) × b × c / 2 = sin(β) × a × c / 2 = sin(γ) × a × b / 2 |
pinta-ala kahden sivun pituudesta ja niiden välisestä kulmasta |
Muut lähteet
- MAOL-taulukkokirja, Otava, 2000